Generate Video Variations - No dataset or deep learning required!

Watch the video and see more examples!

Have you ever wanted to edit a video?

Remove or add someone, change the background, make it last a bit longer, or change the resolution to fit a specific aspect ratio without compressing or stretching it. For those of you who already ran advertisement campaigns, you certainly wanted to have variations of your videos for AB testing and see what works best. Well, this new research by Niv Haim et al. can help you do all of these out of a single video and in HD! Indeed, using a simple video, you can perform any tasks I just mentioned in seconds or a few minutes for high-quality videos. You can basically use it for any video manipulation or video generation application you have in mind. It even outperforms GANs in all ways and doesn’t use any deep learning fancy research nor requires a huge and impractical dataset! And the best thing is that this technique is scalable to high-resolution videos. It is not only for research purposes with 256x256 pixel videos! Oh, and of course, you can also use it with images [2]! Let’s see how it works.

How does it work?

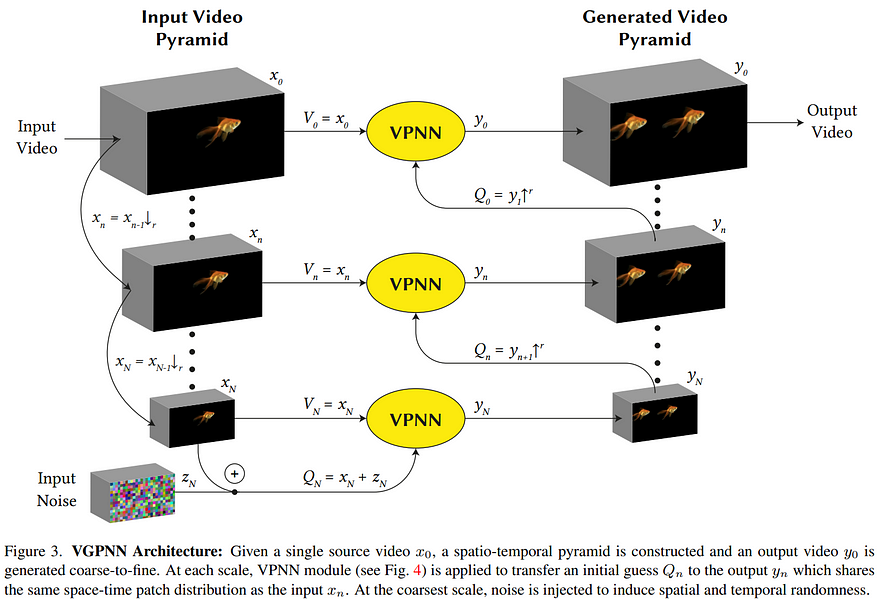
The model is called Video-Based Generative Patch Nearest Neighbors, or VGPNN. Instead of using complex algorithms and models like GANs or transformers, the researchers that developed VGPNN opted for a much simpler approach but revisited. The nearest neighbor algorithm.

First, they downscale the image in a pyramid way, where each level is of lower resolution than the one above. Then, they add random noise to the coarsest level to generate a different image, similar to what GANs do in the compressed space after encoding the image.

Note that here I will say image for simplicity, but in this case, since it is applied to videos, the process is made on 3-frames simultaneously, adding a time dimension, but the explanation stays the same with an extra step at the end.

The image at the coarsest scale with noise added is divided into multiple small square patches. All patches in the image with noise added are replaced with the most similar patch from the initial scaled-down image without noise. This most similar patch is measure with the nearest neighbor algorithm, as we will see. Most of these patches will stay the same, but depending on the added noise, some patches will change just enough to make them look more similar to another patch in the initial image.

This is the VPNN output you see above. These changes are just enough to generate a new version of the image. Then, this first output is upscaled and used to compare with the input image of the next scale to act as a noisy version of it, and the same steps are repeated in this next iteration. We split these images into small patches and replace the previously generated ones with the most similar ones at the current step.

Let’s get into this VPNN module we just covered:

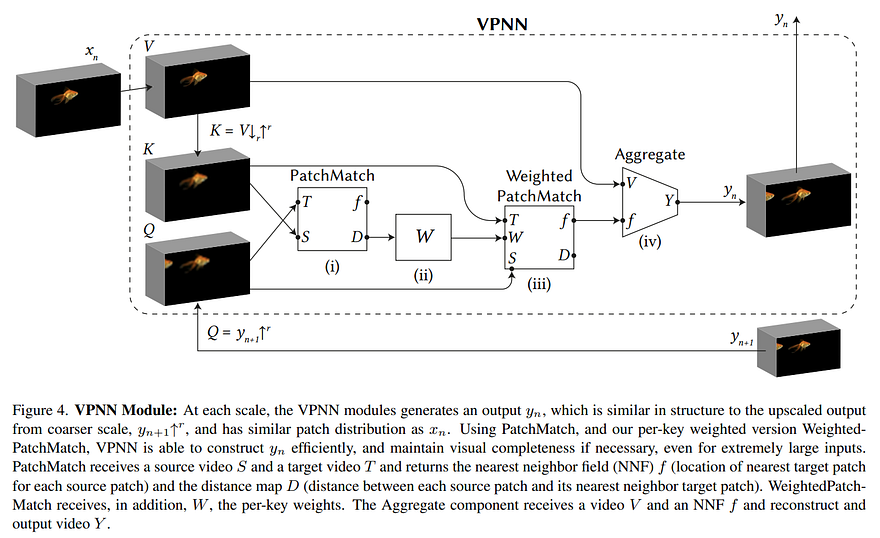
As you can see here, the only difference from the initial step with noise added is that we compare the upscaled generated image, here denoted as Q, with an upscaled version of the previous image just so it has the same level of details and sharpness, denoted as K. Basically, using the level below as comparisons, we compare Q and K and then select corresponding patches in the image from this current level, V, to generate the new image for this step, which will be used for the next iteration. As you see here with the small arrows, K is just an upscaled version of the image we created downscaling V in the initial step of this algorithm, where we created the pyramidal-scaling versions of our image. This is done to compare the same level of sharpness in both images as the upscaled generated image from the previous layer (Q) would be much more blurry than the image at the current step (V), and it would be hard to find similar patches. And this is repeated until we get back to the top of the pyramid with high-resolution results. Then, all these generated patches are folded into a video.

Summary

Let’s do a quick summary:
The image is downscaled at multiple scales. Noise is added to the coarsest-scale image, which is divided into small square patches. Each noisy patch is then replaced with the most similar patches from the same compressed image without noise, causing few random changes in the image while keeping realism. Both the newly generated image and image without the noise of this step are upscaled and compared to find the most similar patches with the nearest neighbor again. These most similar patches are then chosen from the image at the current resolution to generate a new image for this step. And we repeat these upscaling and comparing steps until we get back to the top of the pyramid with high-resolution results.

And voilà! You can repeat this with different noises or modifications to generate any variations you want on your videos!

Limitations

Of course, the results are not perfect. You can still see some artifacts like people appearing and disappearing at weird places or simply copy-pasting someone in some cases, making it very obvious if you focus on it. Still, it’s only the first paper attacking video manipulations with the nearest neighbor algorithm and making it scalable to high-resolution videos. It is always awesome to see different approaches. I’m super excited to see the next paper improving upon this one!

Also, the results are still quite impressive, and they could be used as a data augmentation tool for models working on videos due to their very low runtime. Allowing other models to train on larger and more diverse datasets without much cost.

If you are interested in learning more about this technique, I would strongly recommend reading their paper [1].

Thank you for reading!

If you like my work and want to stay up-to-date with AI, you should definitely follow me on my other social media accounts (LinkedIn, Twitter) and subscribe to my weekly AI newsletter!

To support me:

• The best way to support me is by being a member of this website or subscribe to my channel on YouTube if you like the video format.
• Support my work financially on Patreon.
• Follow me here on medium or here on my blog.

References

[1] Paper covered: Haim, N., Feinstein, B., Granot, N., Shocher, A., Bagon, S., Dekel, T., & Irani, M. (2021). Diverse Generation from a Single Video Made Possible. ArXiv, abs/2109.08591.

[2] The technique that was adapted from images to videos: Niv Granot, Ben Feinstein, Assaf Shocher, Shai Bagon, and Michal Irani. Drop the gan: In defense of patches nearest neighbors as single image generative models. arXiv preprint arXiv:2103.15545, 2021.

[3] Code (available soon): https://nivha.github.io/vgpnn/